Title: An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling
对于大多数深度学习从业者来说,序列建模是循环网络的代名词。然而最近的结果表明,卷积架构在音频合成和机器翻译等任务上的性能优于循环网络。给定一个新的序列建模任务或数据集,应该使用哪种架构?我们对用于序列建模的通用卷积和循环架构进行了系统评估。这些模型在广泛的标准任务中进行评估,这些标准任务通常用于对循环网络进行基准测试。我们的结果表明,简单的卷积架构在各种任务和数据集上都优于典型的循环网络,例如 LSTM,同时展示了更长的有效记忆。我们得出结论,应该重新考虑序列建模和循环网络之间的共同关联,并且应该将卷积网络视为序列建模任务的自然起点。为了协助相关工作,我们在 http://github.com/locuslab/TCN 上提供了代码。
引言
深度学习从业者通常将循环架构视为序列建模任务的默认起点。 深度学习规范教科书中的序列建模章节标题为“序列建模:递归和循环网络”,捕捉了序列建模和递归架构的共同关联。 近期备受好评的“序列模型”在线课程专注于循环架构。
另一方面,最近的研究表明,某些卷积架构可以在音频合成、词级语言建模和机器翻译方面达到最先进的精度。 这就提出了一个问题,卷积序列建模的这些成功是否仅限于特定的应用领域,或者是否需要对序列处理和循环网络之间的关联进行更广泛的重新考虑。
我们通过对广泛的序列建模任务的卷积和循环架构进行系统的经验评估来解决这个问题。 我们专门针对一组全面的任务,这些任务已被反复用于比较不同循环网络架构的有效性。 这些任务包括复调音乐建模、单词和字符级别的语言建模,以及经过精心设计并经常用于基准 RNN 的合成压力测试。 因此,我们的评估旨在比较卷积和循环方法在循环网络的“主场”上进行序列建模。
为了表示卷积网络,我们描述了一种适用于所有任务的通用时间卷积网络 (TCN) 架构。 这种架构是由最近的研究提供的,但故意保持简单,结合了现代卷积架构的一些最佳实践。 它与 LSTM 和 GRU 等规范的循环架构进行了比较。
结果表明,在广泛的序列建模任务中,TCN 令人信服地优于基线循环架构。 这一点尤其值得注意,因为这些任务包括通常用于评估循环网络设计的各种基准。 这表明最近卷积架构在音频处理等应用中的成功并不局限于这些领域。
为了进一步理解这些结果,我们更深入地分析了循环网络的记忆保留特性。 我们表明,尽管循环架构具有捕获无限长历史的理论能力,但 TCN 表现出更长的内存,因此更适合需要长历史的领域。
据我们所知,所提出的研究是对序列建模任务上的卷积和循环架构进行的最广泛的系统比较。 结果表明,应该重新考虑序列建模和循环网络之间的共同关联。 TCN 架构看起来不仅比 LSTM 和 GRU 等规范循环网络更准确,而且更简单、更清晰。 因此,它可能是将深度网络应用于序列的更合适的起点。
背景
几十年来,卷积网络已应用于序列。 它们在 80 年代和 90 年代主要用于语音识别。 ConvNets 随后被应用于 NLP 任务,例如词性标注和语义角色标注。 最近,卷积网络被应用于句子分类和文档分类。 对我们的工作特别鼓舞人心的是最近将卷积架构应用于机器翻译、音频合成和语言建模。
循环网络是专用的序列模型,它维护一个随时间传播的隐藏激活向量。由于在语言建模和机器翻译。循环建模的直观吸引力在于,隐藏状态可以作为迄今为止在序列中看到的所有内容的表示。众所周知,基本的 RNN 架构难以训练,而通常使用更复杂的架构,例如 LSTM 和 GRU 。许多其他用于循环网络的架构创新和训练技术已经被引入并继续积极探索。
已经进行了多项实证研究来评估不同循环架构的有效性。这些研究的部分动机是此类架构设计中的许多自由度。钟等人在复调音乐建模任务中比较了不同类型的循环单元(LSTM 与 GRU)。帕斯卡努等人探索了构建深度 RNN 的不同方法,并评估了不同架构在复调音乐建模、字符级语言建模和单词级语言建模方面的性能。 Jozefowicz 等人搜索了一万多个不同的 RNN 架构,并评估了它们在各种任务上的性能。他们得出的结论是,如果存在“比 LSTM 更好的架构”,那么它们“并非易事”。格雷夫等人对八种 LSTM 变体在语音识别、手写识别和和弦音乐建模方面的性能进行了基准测试。他们还发现“没有一个变体可以显着改进标准 LSTM 架构”。张等人系统地分析了 RNN 的连接架构,并评估了字符级语言建模和合成压力测试的不同架构。梅利斯等人在词级和字符级语言建模上对基于 LSTM 的架构进行了基准测试,并得出结论“LSTM 优于最新模型”。
最近的其他工作旨在结合 RNN 和 CNN 架构的各个方面。 这包括卷积 LSTM,它将 LSTM 中的全连接层替换为卷积层,以允许在循环层中添加额外的结构; Quasi-RNN 模型,将卷积层与简单的循环层交错;扩张的 RNN ,它为循环架构增加了扩张。 虽然这些组合在结合两种架构的理想方面方面显示出希望,但我们在这里的研究重点是比较通用卷积和循环架构。
尽管已经对具有代表性的序列建模任务的 RNN 架构进行了多次彻底的评估,但我们不知道对序列建模的卷积和循环方法进行了类似的彻底比较。(有论文用于句子级和文档级分类任务的卷积网络和循环网络的比较。相比之下,序列建模需要能够逐个元素合成整个序列的架构。)这种比较是鉴于上述卷积架构在该领域取得的近期成功,这尤其令人感兴趣。 我们的工作旨在比较典型序列建模任务上的通用卷积和循环架构,这些任务通常用于对 RNN 变体本身进行基准测试。
时间卷积网络
首先描述卷积序列预测的通用架构。我们的目标是将卷积网络设计中的最佳实践提炼成一个简单的架构,可以作为一个方便但强大的起点。我们将所呈现的架构称为时间卷积网络 (TCN),强调我们采用该术语不是作为真正新架构的标签,而是作为一系列架构的简单描述性术语。(请注意,该术语之前已使用过。) TCN 的显着特征是:
- 架构中的卷积是因果关系,这意味着没有从未来到过去的信息“泄漏”;
- 该架构可以采用任意长度的序列并将其映射到相同长度的输出序列,就像使用 RNN 一样。
除此之外,我们强调如何使用非常深的网络(通过残差层增强)和扩张卷积来构建非常长的有效历史大小 (即网络能够查看非常远的过去进行预测) 。
我们的架构受到最近用于序列数据的卷积架构的启发,但不同于所有的它们中的一个,是根据第一原理设计的,结合了简单性、自回归预测和非常长的记忆。 例如,TCN 比 WaveNet 简单得多(没有跨层的跳过连接、调节、上下文堆叠或门控激活)。
与 Dauphin 等人的语言建模架构相比,TCN 不使用门控机制并且具有更长的内存。
序列建模
在定义网络结构之前,我们强调序列建模任务的性质。 假设给定一个输入序列 ,并希望预测一些相应的输出 。 关键约束是要预测某个时间 的输出 ,我们被限制为仅使用之前观察到的那些输入。 形式上,序列建模网络是任何生成映射 的函数:
如果它满足 仅取决于 的因果约束,而不是任何“未来”输入 。 在序列建模设置中学习的目标是找到一个网络 最小化实际输出和预测之间的一些预期损失 , 其中序列和输出是根据某种分布绘制的。
这种形式主义包含许多设置,例如自回归预测(我们尝试在给定过去的情况下预测某些信号),通过将目标输出设置为简单地移动一个时间步长的输入。 然而,它并不直接捕获机器翻译或序列到序列预测等领域,因为在这些情况下,整个输入序列(包括“未来”状态)可用于预测每个输出(尽管这些技术自然可以 扩展到在这样的环境中工作)。
因果卷积
如上所述,TCN 基于两个原则:网络产生与输入长度相同的输出,以及不能从未来泄漏到过去。 为了完成第一点,TCN 使用一维全卷积网络 (FCN) 架构,其中每个隐藏层的长度与输入层相同,长度填上零填充(内核大小为 1) 以保持后续层的长度与之前的层相同。 为了实现第二点,TCN 使用因果卷积,即时间 的输出仅与时间 和前一层中更早的元素进行卷积的卷积。
简而言之:TCN = 1D FCN + Causal Convolution
请注意,这与近 30 年前由 Waibel 等人提出的时间延迟神经网络架构本质上是相同的。 通过零填充的唯一调整来确保所有层的大小相等。
这种基本设计的一个主要缺点是,为了获得较长的有效历史大小,我们需要一个非常深的网络或非常大的过滤器,这两种方法在最初引入这些方法时都不是特别可行。 因此,在以下部分中,我们将描述如何将现代卷积架构的技术集成到 TCN 中,以允许非常深的网络和非常长的有效历史。
扩张卷积
一个简单的因果卷积只能回顾网络深度中大小线性的历史。 这使得将上述因果卷积应用于序列任务,尤其是那些需要较长历史的任务变得具有挑战性。 我们在这里的解决方案,遵循 van den Oord 等人的工作,使用扩张卷积来实现指数级大的感受野。 更正式地说,对于一维序列输入 和一个滤波器 ,对序列元素 的扩张卷积运算 定义为:
其中 是膨胀因子, 是滤波器大小, 代表过去的方向。 因此,膨胀等效于在每两个相邻的滤波器位置之间引入一个固定步长。 当 时,空洞卷积减少为常规卷积。 使用更大的膨胀使得顶层的输出能够代表更广泛的输入,从而有效地扩展了 ConvNet 的感受野。
这为我们提供了两种增加 TCN 感受野的方法:选择更大的滤波器大小 和增加膨胀因子 ,其中一个这样的层的有效历史是 。 在使用扩张卷积时很常见,我们随着网络的深度呈指数增加 (即在网络的第 层,)。 这确保了有一些过滤器会命中有效历史记录中的每个输入,同时还允许使用深度网络获得非常大的有效历史记录。 我们在图 1(a) 中提供了一个说明。
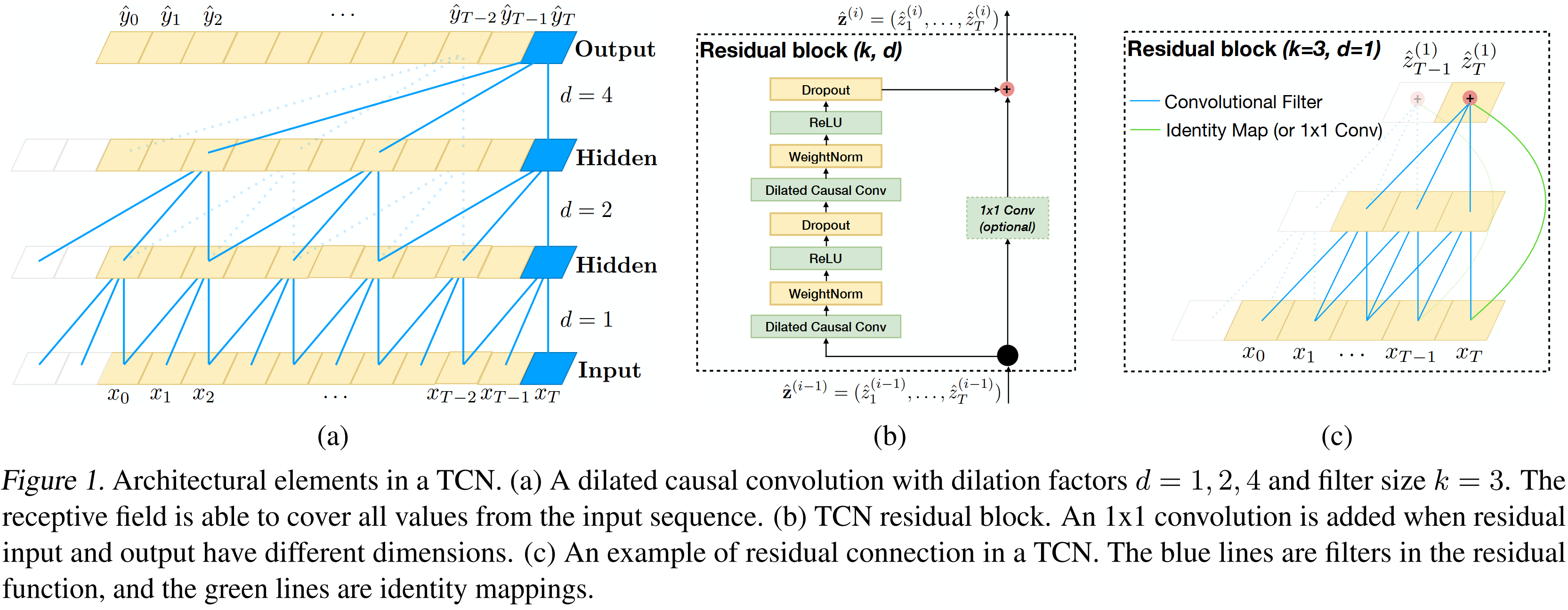
残差连接
残差块包含一个分支,引出一系列转换 ,其输出被添加到块的输入 :
这有效地允许层学习对身份映射的修改,而不是整个转换,这已被反复证明有利于非常深的网络。
由于 TCN 的感受野取决于网络深度 以及滤波器大小 和膨胀因子 ,因此更深和更大的 TCN 的稳定性变得很重要。 例如,在预测可能取决于大小为 的历史和高维输入序列的情况下,可能需要多达 12 层的网络。 更具体地说,每一层由用于特征提取的多个过滤器组成。 因此,在我们设计通用 TCN 模型时,我们使用通用残差模块代替卷积层。
我们的基线 TCN 的残差块如图 1(b) 所示。 在残差块内,TCN 有两层扩张因果卷积和非线性,为此我们使用了整流线性单元 (ReLU)。 对于归一化,我们将权重归一化应用于卷积滤波器。 此外,在每个扩张卷积之后添加了空间 dropout 以进行正则化:在每个训练步骤中,将整个通道归零。
然而,在标准 ResNet 中,输入直接添加到残差函数的输出中,而在 TCN(以及一般的 ConvNets)中,输入和输出可能具有不同的宽度。 为了考虑不同的输入输出宽度,我们使用额外的 1x1 卷积来确保元素加法 接收相同形状的张量(参见图 1(b,c))。
讨论
我们通过列出使用 TCN 进行序列建模的几个优点和缺点来结束本节。
- 并行性:与在 RNN 中对后续时间步的预测必须等待其前任完成的情况不同,卷积可以并行完成,因为每一层都使用相同的过滤器。 因此,在训练和评估中,长输入序列可以在 TCN 中作为一个整体进行处理,而不是像在 RNN 中那样按顺序处理。
- 灵活的感受野大小:TCN 可以通过多种方式改变其感受野大小。 例如,堆叠更多扩张(因果)卷积层、使用更大的扩张因子或增加过滤器大小都是可行的选择(可能有不同的解释)。 因此,TCN 可以更好地控制模型的内存大小,并且易于适应不同的领域。
- 稳定的梯度: 与循环架构不同,TCN 的反向传播路径与序列的时间方向不同。 因此,TCN 避免了梯度爆炸/消失的问题,这是 RNN 的一个主要问题(并导致了 LSTM、GRU、HF-RNN 等的发展)。
- 训练时内存要求低:特别是在输入序列较长的情况下,LSTM 和 GRU 很容易占用大量内存来存储它们的多个单元门的部分结果。 然而,在 TCN 中,过滤器跨层共享,反向传播路径仅取决于网络深度。 因此,在实践中,我们发现门控 RNN 可能比 TCN 使用更多的内存。
- 可变长度输入: 就像 RNN 以循环方式对可变长度的输入进行建模一样,TCN 也可以通过滑动 1D 卷积核来接收任意长度的输入。 这意味着 TCN 可以作为 RNN 的替代品,用于任意长度的序列数据。
使用 TCN 也有两个明显的缺点。
- 评估期间的数据存储:在评估/测试中,RNN 只需保持隐藏状态并获取当前输入 xt 即可生成预测。 换句话说,整个历史的“摘要”由一组固定长度的向量 ht 提供,而实际观察到的序列可以被丢弃。 相比之下,TCN 需要接收到有效历史长度的原始序列,因此在评估期间可能需要更多内存。
- 域转移的潜在参数变化:不同领域对模型预测所需的历史数量可能有不同的要求。 因此,当将模型从只需要很少内存的域(即小的 和 )转移到需要更长内存的域(即大得多的 和 )时,TCN 可能会因为没有 足够大的感受野。





评论区