Title: Spectral Temporal Graph Neural Network for Multivariate Time-series Forecasting
多变量时间序列预测在许多实际应用中起着至关重要的作用。这是一个具有挑战性的问题,因为需要同时考虑变量内时间相关性和变量间相关性。最近,有多项工作试图捕捉这两种相关性,但大多数(如果不是全部)只捕捉时域中的时间相关性,并采用预定义的先验作为系列间的关系。在本文中,我们提出了频谱时间图神经网络 (StemGNN),以进一步提高多变量时间序列预测的准确性。 StemGNN 在谱域中联合捕获系列间相关性和时间依赖性。它结合了对变量间相关性进行建模的图傅里叶变换 (GFT) 和在端到端框架中对时间依赖性进行建模的离散傅里叶变换 (DFT)。通过 GFT 和 DFT 后,谱表示具有清晰的模式,可以通过卷积和顺序学习模块进行有效预测。此外,StemGNN 自动从数据中学习序列间相关性,而无需使用预定义的先验。我们对十个真实世界的数据集进行了广泛的实验,以证明 StemGNN 的有效性。
引言
时间序列预测在各种现实世界场景中发挥着至关重要的作用,例如交通预测、供应链管理和金融投资。 如果可以准确估计事件或指标的未来演变,它可以帮助人们做出重要决策。 例如,如果提前预计会出现严重的交通拥堵,我们可以修改我们的行车路线或重新安排预约。 此外,如果我们能够提前预测 COVID-19 的趋势,我们就能够重新安排重要事件并迅速采取行动来防止流行病的传播。
基于历史时间序列数据进行准确预测具有挑战性,因为需要联合建模系列内时间模式和系列间相关性。最近,深度学习模型对这个问题有了新的认识。一方面,长短期记忆 (LSTM)、门控循环单元 (GRU)、门控线性单元 (GLU) 和时间卷积网络 (TCN) 在以下方面取得了可喜的成果时间建模。同时,离散傅里叶变换 (DFT) 也可用于时间序列分析。例如,状态频率记忆 (SFM) 网络结合了 DFT 和 LSTM 的优点,用于股票价格预测;光谱残差 (SR) 模型利用 DFT 并在时间序列异常检测中实现了最先进的性能。多元时间序列预测的另一个重要方面是对多个时间序列之间的相关性进行建模。例如,在交通预测任务中,相邻的道路自然会相互影响。当前最先进的模型高度依赖图卷积网络 (GCN),源于图傅里叶变换(GFT)理论。这些模型直接堆叠 GCN 和时间模块(例如 LSTM、GRU),它们仅捕获时域中的时间模式,并且需要预定义的变量间关系拓扑。
在本文中,我们的目标是更好地联合建模变量内时间模式和变量间相关性。具体来说,我们希望结合 GFT 和 DFT 的优点,并完全在谱域中对多变量时间序列数据进行建模。直觉是,在 GFT 和 DFT 之后,光谱表示可以保持更清晰的模式并且可以更有效地预测。实现这一目标并非易事。这项工作的关键技术贡献是精心设计的 StemGNN(频谱时间图神经网络)块。在 StemGNN 块中,首先应用 GFT 将结构化多变量输入转换为谱时间序列表示,而不同的趋势可以分解为正交时间序列。此外,利用 DFT 将每个单变量时间序列转换为频域。在 GFT 和 DFT 之后,谱表示变得更容易被卷积和序列建模层识别。此外,在端到端框架中加入了一个潜在的相关层来自动学习系列间的相关性,因此它不需要多变量依赖作为先验。此外,我们采用具有共享编码器的预测和回溯输出模块来促进多元时间序列的表示能力。
论文的主要贡献总结如下:
- StemGNN 是第一个在谱域中联合表示变量内和变量间相关性的工作。 它同时和协作地封装了 GFT、DFT 和深度神经网络的优点。 消融研究进一步证明了这种设计的有效性。
- StemGNN 可以为不同的时间序列构建依赖图的数据驱动。 因此,该模型对于所有没有预定义拓扑的多变量时间序列都是通用的。 如实验所示,自动学习的图结构具有良好的可解释性,并且比人类定义的图结构工作得更好。
- StemGNN 在多变量时间序列预测的九个公共基准上实现了最先进的性能。 平均而言,它在 MAE 上比最佳基线高 8.1%,在 RMSE 上高出 13.3%。 关于 COVID-19 的案例研究进一步显示了其在实际场景中的可行性。
相关工作
时间序列预测是机器学习中的一个新兴话题,可分为两大类:单变量技术 和多变量技术。 单变量技术分别分析每个单独的时间序列,而不考虑不同时间序列之间的相关性。 例如,FC-LSTM预测具有 LSTM 和全连接层的单变量时间序列。 SMF 通过离散傅里叶变换 (DFT) 将给定单变量时间序列的单元状态分解为一系列不同的频率分量,从而改进了 LSTM 模型。 N-BEATS提出了一种深度神经架构,该架构基于具有基础扩展的全连接层的深度堆栈。
多变量技术将多个时间序列的集合视为一个统一的实体。 TCN是该类别中的代表作,将高维数据完全视为张量输入,并通过扩张卷积考虑大的感受野。 LSTNet使用卷积神经网络 (CNN) 和循环神经网络 (RNN) 来提取变量之间的短期局部依赖模式并发现时间序列的长期模式。 DeepState 将状态空间模型与深度递归神经网络结合起来,通过最大对数似然学习整个网络的参数。 DeepGLO 在训练和预测期间利用全局和局部特征。 DeepGLO 中的全局组件基于矩阵分解,能够通过将每个时间序列表示为基本组件的线性组合来捕获全局模式。还有一类作品使用图神经网络来明确捕捉不同时间序列之间的相关性。例如,DCRNN 在用于交通预测的卷积递归神经网络中结合了空间和时间依赖性。 ST-GCN 是另一个用于流量预测的深度学习框架,通过时空卷积块集成图卷积和门控时间卷积。 GraphWaveNet 将图卷积层与自适应邻接矩阵和扩张的随机卷积相结合,以捕获时空依赖性。然而,它们中的大多数要么忽略系列间的相关性,要么需要依赖图作为先验。此外,尽管傅立叶变换在以前的工作中已经显示出其优势,但现有的解决方案都没有在谱域中联合捕获时间模式和多变量依赖关系。
问题定义
为了强调多个时间序列之间的关系,我们基于称为多变量时间图的数据结构制定了多变量时间序列预测问题,可以表示为 。代表多变量时间序列输入,其中 是多变量时间序列(节点)的数量, 是时间步的数量。我们将时间戳 处的观测值表示为 。 为邻接矩阵,其中表示有一条边连接节点和,表示这条边的强度。
给定先前 个时间戳 的观测值,多变量时间序列预测的任务旨在预测下一个 $H $个时间戳的多变量时间图 中的节点值,记为 。这些值可以通过带有参数 和图结构 的预测模型 推断出来,其中 可以作为先验输入或从数据中自动推断出来。
频谱时间图神经网络
概述
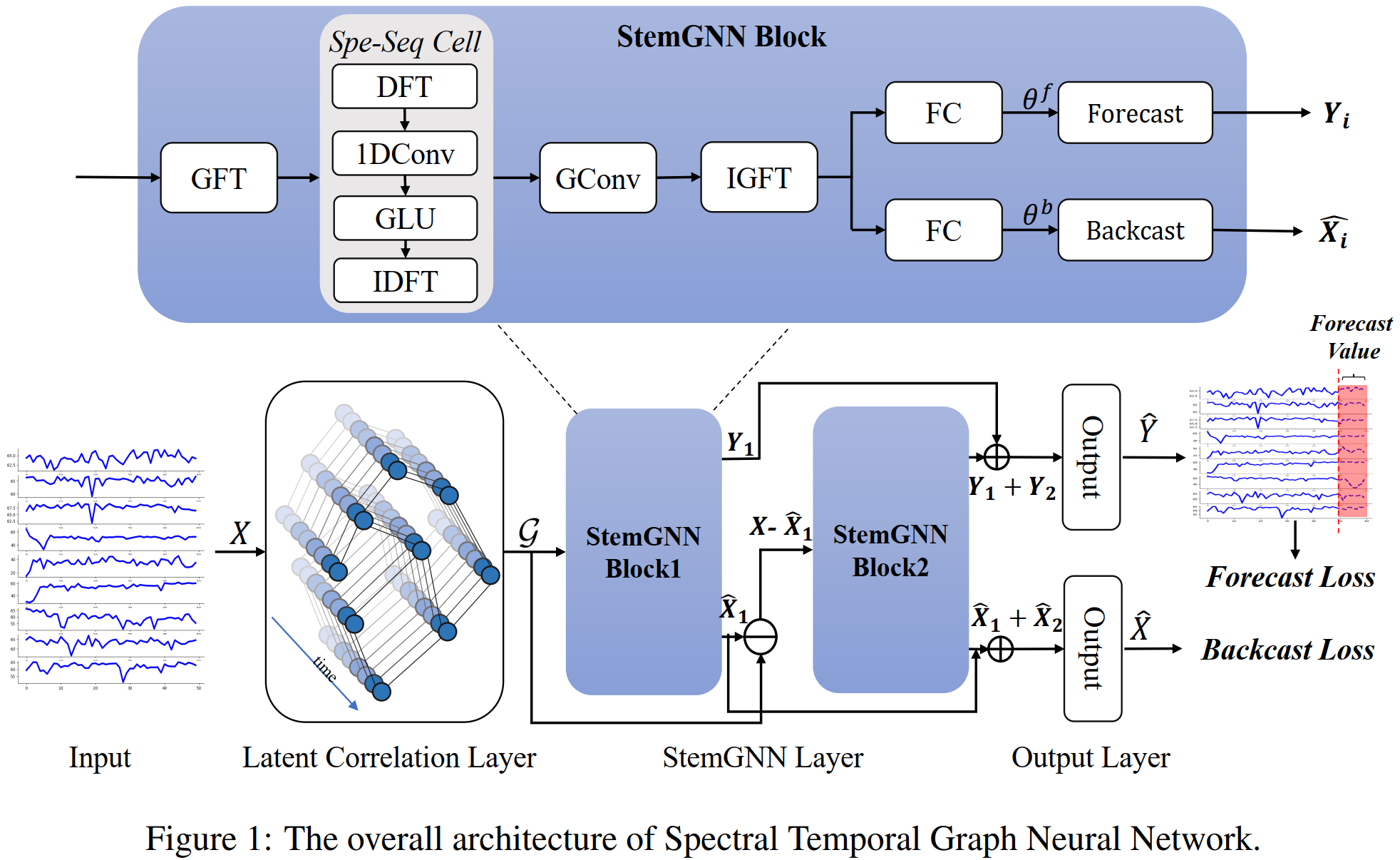
在这里,我们提出频谱时间图神经网络 (StemGNN) 作为多元时间序列预测的通用解决方案。 StemGNN 的整体架构如图 1 所示。多变量时间序列输入 首先被送到潜在相关层,其中可以从数据中自动推断出图结构及其相关的权重矩阵 。
接下来,图 作为由两个残差 StemGNN 块组成的 StemGNN 层的输入。 StemGNN 块的设计目的是在频谱域中联合建模多变量时间序列内的结构和时间依赖性(如图 1 所示)。 它包含一系列精心设计的运算符。 首先,图傅里叶变换 (GFT) 算子将图 转换为谱矩阵表示,其中每个节点的单变量时间序列变为线性独立。 然后,离散傅里叶变换 (DFT) 算子将每个单变量时间序列分量变换到频域。 在频域中,表示被输入一维卷积和 GLU 子层以捕获特征模式,然后通过逆 DFT 转换回时域。 最后,我们在谱矩阵表示上应用图卷积并执行逆 GFT。
在 StemGNN 层之后,我们添加了一个由 GLU 和全连接 (FC) 子层组成的输出层。 网络中有两种输出。 预测输出 被训练以生成对未来值的最佳估计,而回溯输出 以自动编码方式使用以增强多元时间序列的表示能力。 最终的损失函数可以表示为预测损失和回溯损失的组合:
其中第一项表示预测损失,第二项表示回溯损失。 对于每个时间戳 , 是滑动窗口内的输入值, 是要预测的真实值, 是时间戳 的预测值, 是来自回溯模块的重构值。 表示产生回溯输出的整个网络, 表示网络中的所有参数。
在推理阶段,采用滚动策略进行多步预测。 首先,通过将 作为输入来预测 。 然后,输入将变为 用于预测下一个时间戳 。 通过连续应用这种滚动策略,我们可以获得下一个 个时间戳的预测值。
潜在相关层 Latent Correlation Layer
在对多变量时间序列进行建模时,基于 GNN 的方法需要图结构。 它可以通过人类知识构建(例如交通预测中的道路网络),但有时我们没有预先定义的图结构。 为了服务于一般情况,我们利用自注意力机制自动学习多个时间序列之间的潜在相关性。 通过这种方式,该模型以数据驱动的方式强调了特定于任务的相关性。
首先,输入 被送入一个门控循环单元(GRU)层,该层依次计算每个时间戳 t 对应的隐藏状态。 然后,我们使用最后一个隐藏状态 R 作为整个时间序列的表示,并通过自注意机制计算权重矩阵 W,如下所示:
其中 和 表示 query 和 key 的表示,可以分别通过注意力机制中具有可学习参数 和 的线性投影来计算; 是 和 的隐藏维度大小。输出矩阵 作为图 的邻接权重矩阵。self-attention 的整体时间复杂度为 。
StemGNN 块
StemGNN 层是通过堆叠多个带有跳过连接的 StemGNN 块来构建的。 通过将频谱序列 (Spe-Seq) 单元嵌入到频谱图卷积模块中来设计 StemGNN 块。 在本节中,我们首先介绍 StemGNN 块的动机和架构,然后分别简要描述 Spe-Seq Cell 和 Spectral Graph Convolution 模块。
StemGNN Block
谱图卷积因其在谱域中学习多个时间序列的潜在表示的非凡能力而被广泛用于时间序列预测任务。 关键组件是应用图傅里叶变换 (GFT) 来捕获序列间的关系。 值得注意的是,GFT 的输出也是一个多变量时间序列,而 GFT 并没有显式地学习序列内时间关系。 因此,我们可以利用离散傅里叶变换 (DFT) 在频域中基于三角函数学习输入时间序列的表示,从而捕获周期性数据中的重复模式或不同时间戳之间的自相关特征。 受此启发,我们将 Spe-Seq Cell 应用于 GFT 的输出以学习频域中的时间模式。 然后 Spe-Seq Cell 的输出由 Spectral Graph Convolution 的其余组件处理。
StemGNN 模型也可以扩展到多个渠道。 我们在输入数据的每个单独通道 上应用 GFT 和 Spe-Seq Cell,并将图卷积后的结果与内核 相加。 接下来,在求和上应用逆图傅里叶变换(IGFT),得到输出的第个通道,可以写成如下,
这里、和分别表示GFT、IGFT和Spe-Seq Cell,是第个输入和第个输出通道对应的图卷积核,是归一化拉普拉斯算子的特征值矩阵和 GFT 中使用的特征向量等价于没有降维的多元维数 ()。 之后,我们连接每个输出通道 以获得最终结果 。
论文作者使用可学习的参数来表示基向量和一个全连接层来生成基于 的基扩展系数 。然后可以通过组合不同的基来计算输出:。 我们在 StemGNN 块中有这个模块的两个分支,一个用于预测未来值,即预测分支,另一个用于重建历史值,即回溯分支(用 表示)。 回溯分支有助于调节块的方法空间来表示时间序列数据。
此外,使用残差连接来堆叠多个 StemGNN 块来构建更深层次的模型。 在例子中,使用了两个 StemGNN 块。 第二个块试图逼近真实值与第一个块的重建值之间的残差。 最后,将两个块的输出连接起来并馈送到 GLU 和全连接层以生成预测。
Spectral Sequential Cell (Spe-Seq Cell)
Spe-Seq Cell 旨在将 GFT 之后的每个单独的时间序列分解为频率基,并在它们上学习特征表示。 它按顺序由四个部分组成:离散傅里叶变换(DFT,)、一维卷积、GLU 和离散傅里叶逆变换(IDFT, ),其中 DFT 和 IDFT 在时域和频域之间转换时间序列数据, 而一维卷积和 GLU 在频域中学习特征表示。 具体来说,DFT 的输出有实部()和虚部(),它们由具有不同参数的相同算子并行处理。 操作可以表述为:
其中 是实验中大小为 3 的卷积核,是 Hadamard 乘积,非线性 sigmoid 门 决定了当前输入中有多少信息与序列模式密切相关。 最后,可以通过 获得结果,并将 IDFT 应用于最终输出。
Spectral Graph Convolution
频谱图卷积由三个步骤组成。 (1) 多变量时间序列输入通过 GFT 投影到频谱域。 (2) 频谱表示由具有可学习内核的图卷积算子过滤。 (3) 对频谱表示应用逆图傅里叶变换 (IGFT) 以生成最终输出。
图傅里叶变换 (GFT) 是频谱图卷积的基本算子。 它将输入图投影到正交空间,其中基由归一化图拉普拉斯算子的特征向量构成。 归一化图拉普拉斯算子 可以计算为:,其中 是单位矩阵, 是 的对角度矩阵。 然后,我们对拉普拉斯矩阵进行特征值分解,形成 ,其中 是特征向量矩阵, 是特征值对角矩阵。 给定多元时间序列 ,GFT 和 IGFT 的算子分别定义为 和 。 图卷积算子实现为特征值矩阵 的函数 ,参数为 。 整体时间复杂度为 。





评论区